..

#gamedev

(Win) 007 - Output Sound With DirectSound

To write a sound output we need initialize the Direct Sound for Windows.

That process I'll cover in another post. In this specific post, I'm going to explain how the buffer works and some important highlights to put sound into sound card.

How the sound works

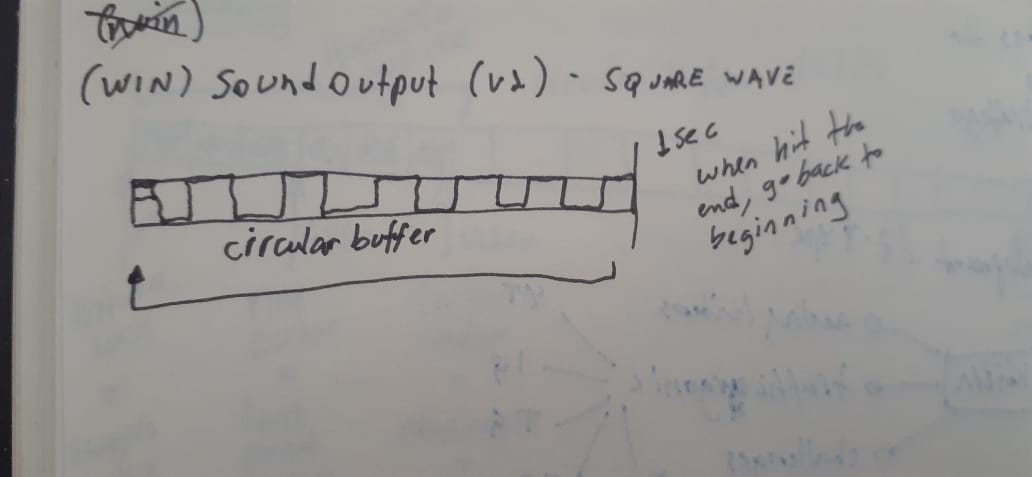
First of all, we need to create a buffer that holds the bytes (samples). This buffer is a circular buffer, which means that we can store one second of data and when write cursor hit the end of buffer, we'll start to write at the beginning of buffer.

1733843701.jpeg

Now, we need to Lock the buffer to get two regions' area to write.

It happens because if the play cursor is before the write cursor, we need to write two regions.

The first is from write cursor until the buffer end. And another from beginning of buffer until play cursor.

If we can store all the bytes into only one region, means that the play cursor is after the write cursor.

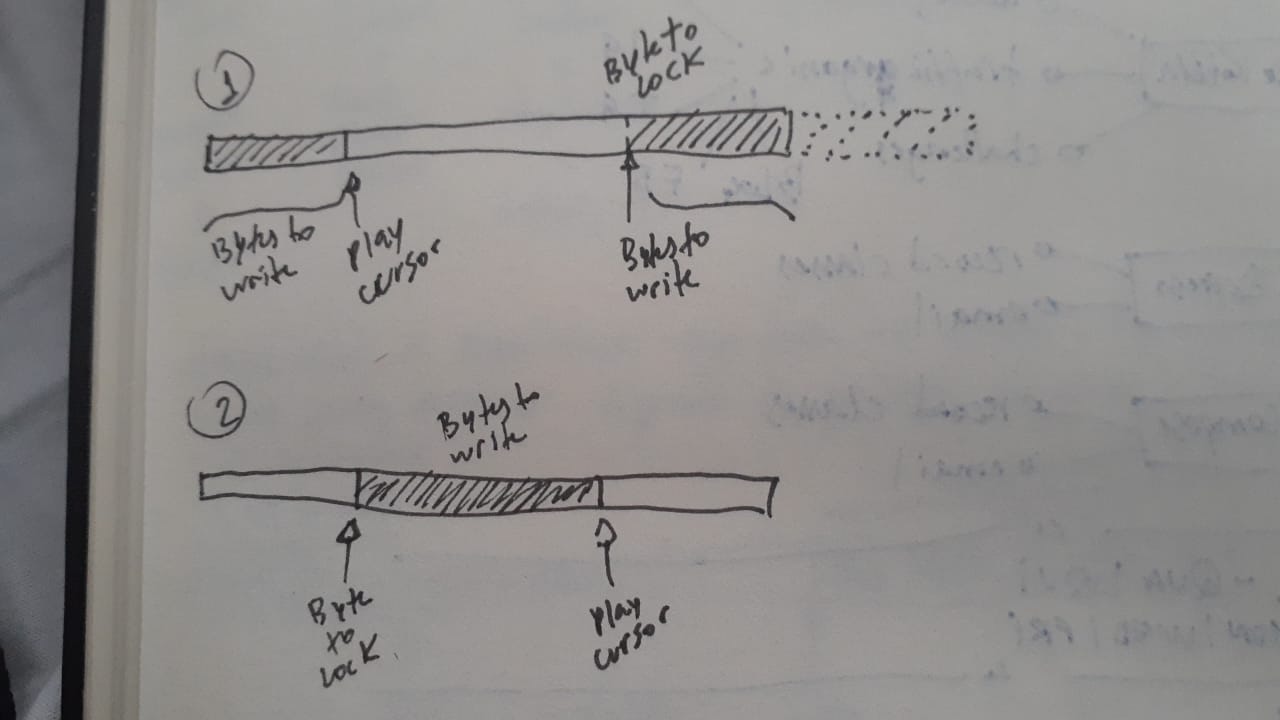
1733844617.jpeg

To do this, we need to use the function IDirectSoundBuffer::Lock.

Fill the buffer

Now we need to iterate through the two (or one) regions to fill it with some data.

The buffer works with 2 channels, each channel has 16 bits (short). So, [LEFT RIGHT] is gonna be a single sample (2 bytes left, 2 bytes right). This make sense for stereo sound.

So, the first thing we want to do is mapping the buffer size to sample count index, now it is in bytes. This way, we can figure out which sample is going to be written. 

int sample_index = 0;
DWORD bytes_per_sample = sizeof(int16) * 2; // 4 bytes

int16 *samples = (int16 *) region1;
DWORD sample_count = region1_size / bytes_per_sample;
for (DWORD i = 0; i < sample_count; i++) {
    *samples++ = LEFT; // let's do later
    *samples++ = RIGHT; // let's do later
    sample_index++;
}

// the same for region2

How to compute Square Wave

Remember, our sound is 48khz. Hertz = cycles / seconds.

note middle C = 261hz = 261 cycles / seconds.

How many samples will be per chunk?

We can figure out the wave period, which is the samples per chunk of entire buffer:

samples_per_second / tone_hz = wave_period;

48000 / 261 = 183 samples;

So, to write 261 waves we need 183 samples or 91 high samples and 91 low samples.

Figure out the Play and Write cursor

Using the function GetCurrentPosition we can find out the play cursor and write cursor to compute the byte to lock and bytes to write.

Let's mapping again, but now we use the bytes value, not sample count.

Let's transform sample_index into bytes to find where we are (in bytes) compare to play cursor or write cursor. 

DWORD byte_to_lock = (sample_index * bytes_per_sample) % buffer_size;

Mod is required here to not overflow the buffer.

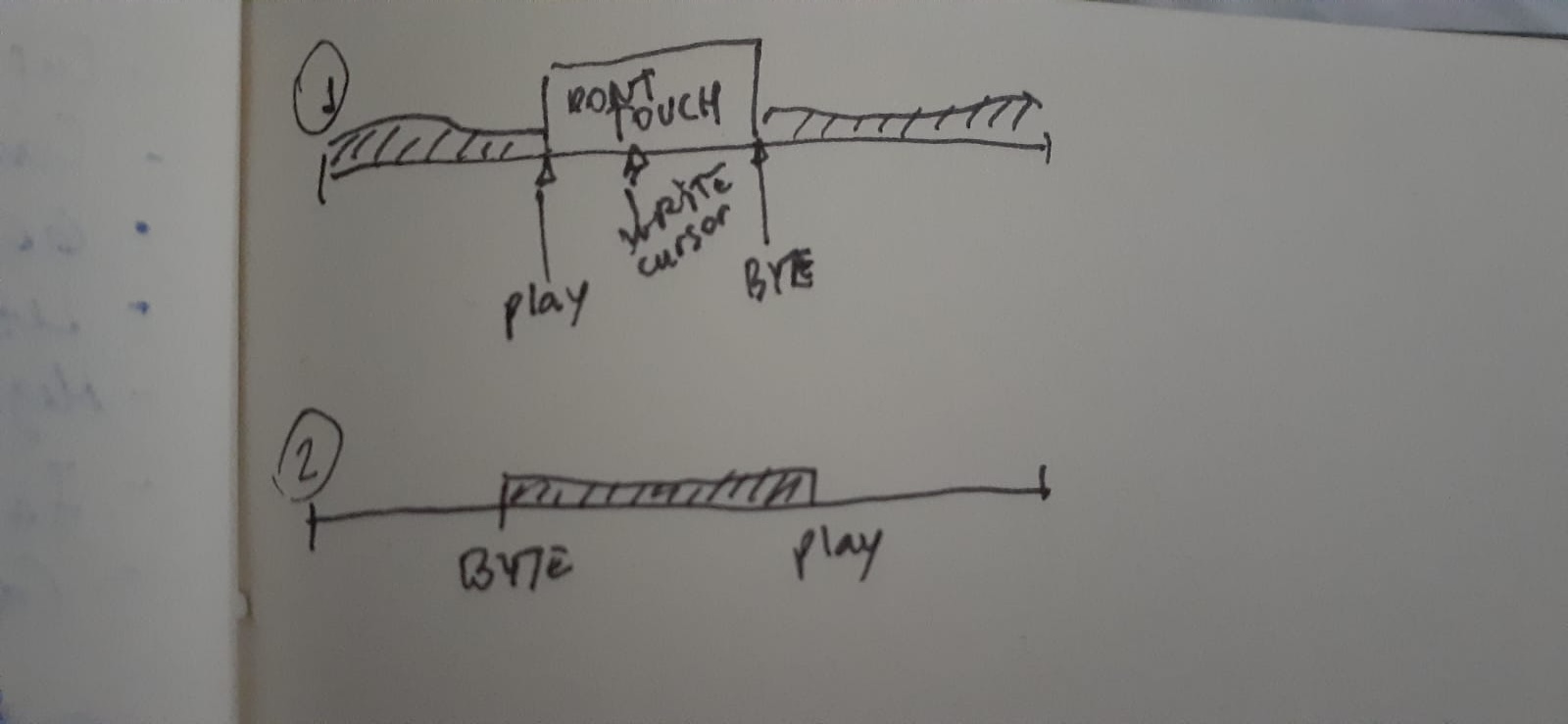
And bytes to write depends on if play cursor is ahead or not. 

if (byte_to_lock > play_cursor) {
    bytes_to_write = buffer_size - play_cursor;
    bytes_to_write += play_cursor;
} else {
    bytes_to_write = play_cursor - byte_to_lock;
}

1733851829.jpeg

Fill one sample based on wave

This is the most complicated part (for me).

We know how many waves to fill in entire second (48.000 khz).

We know how many waves is needed to produce the middle C sound (261 hz).

When we divide samples_per_second / tone_hz, we find how many samples is needed to fill one wave (183 samples).

183 samples represents a single wave period. 91 for higher part, 91 for lower part.

Now, as we know, our sample index as mapped from total buffer size (remember the mod operator). Which means that we know where we are inside the buffer, and now, we know how many samples to filled with high and low volume.

So, let's do sample_index / (wave / 2) to "normalize" our counter until 91 steps AND get the remainder with % operator as image below:

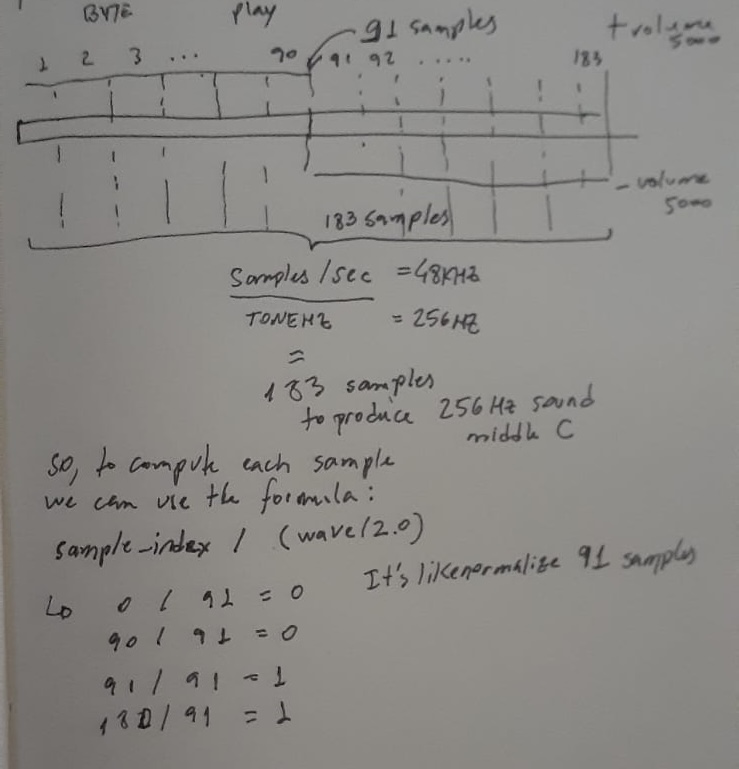
1733852532.jpeg

Now we can compute a square wave that output the middle C sound. 

int16 sample_value = (sample_index / (wave_period / 2) % 2) ? 5000 : -5000;

We can also use the lower bit (1 or 0) to distinguish by up or down. This should be great for performance.

Final adjusts

First, unlock the buffer regions with Unlock function and starts the play with Play function at the beginning of program.

Output Sine Wave

The sine wave can be done by sin(2 * PI * t) as we can see in the next picture:

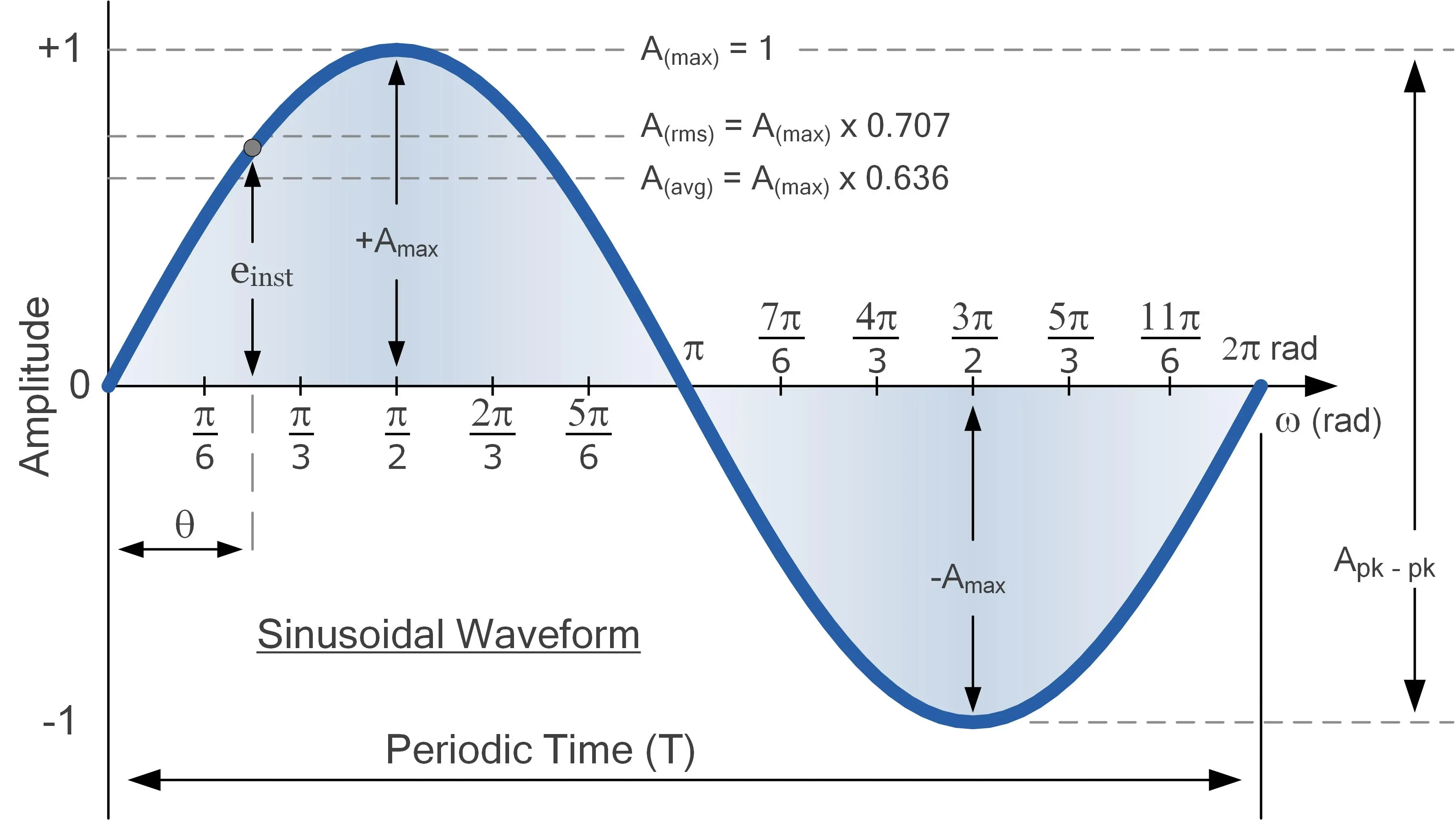
1733947952.webp

So, let's compute the formula with: 

float value = sinf(sound_output->t_sine);
int16 sample_value = (int16) (value * volume);
*samples++ = sample_value;
*samples++ = sample_value;

// increment one sample's worth
sound_output->t_sine += 2.0f * PI * 1.0f / (float) wave_period;

Now, in order not delay the sound after playing, let's fill the entire buffer with some sound at the beginning of program. 

win32_fill_sound_buffer(&sound_ouptput, 0, buffer_size);
secondary_buffer->Play(0, 0, DSBPLAY_LOOPING);

// main loop
DWORD bytes_to_write;
if (byte_to_lock == play_cursor) {
    bytes_to_write = 0;
} else if (byte_to_lock > play_cursor) {
    bytes_to_write = buffer_size - play_cursor;
    bytes_to_write += play_cursor;
} else {
    bytes_to_write = play_cursor - byte_to_lock;
}

win32_fill_sound_buffer(&sound_ouptput, byte_to_lock, bytes_to_write);