How to Rotate a Vector2d

Examples

Today I finally understand how to rotate a vector to make some movement of pixels on the screen.

It is not complicated, but require a little bit of math skills.

Let's get started.

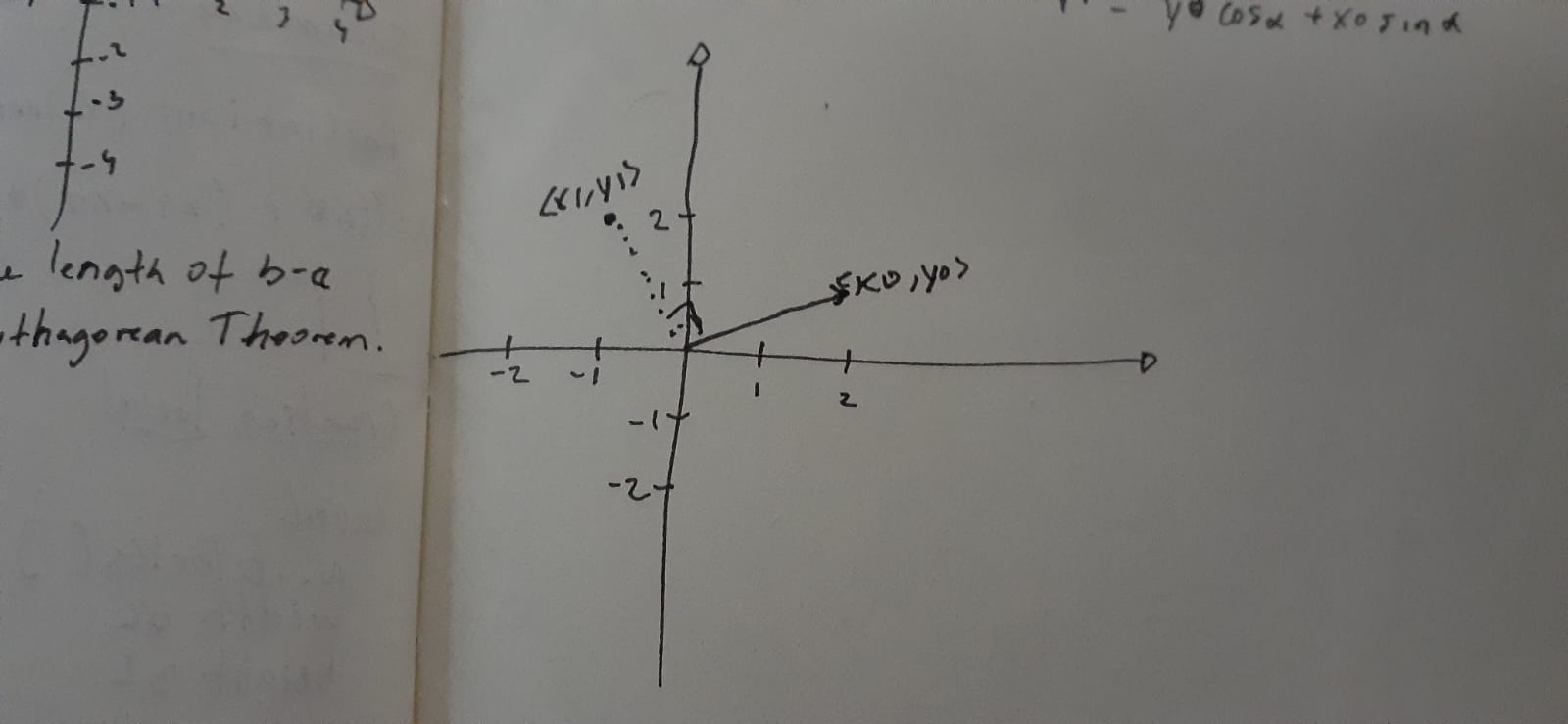
First of all, let's define a arbitrary X and Y point. Let's called it xo,yo. Maybe (1,1).

Mathematically, the vector is define by symbols <xo, yo>. Or a arrow-right at top of vector name.

So, the next image describe the vector 2d into screen.

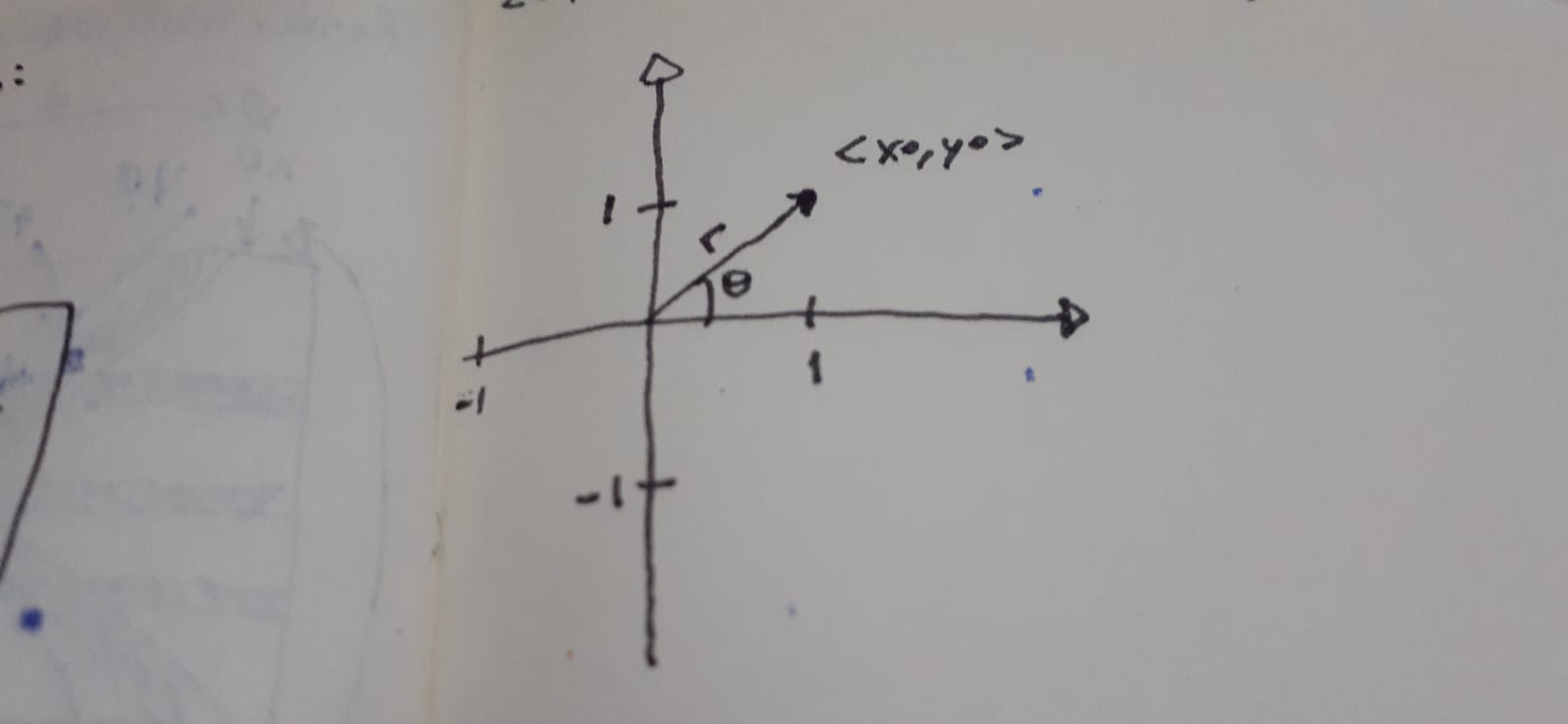
As we can see, the r describe the magnitude/length of vector ||a||.

This value is computed by Pythagorean Theorem. Which is:

rˆ2 = xˆ2 + yˆ2

So, programmatically is something like r = sqrt(x * x + y * y). Which is sqrt(2) = 1,4142.

Now, the value that we'll use to define a new position <x1, y1> is the angle. If we increase the angle, we can change the position, assuming the magnitude of vector is the same.

With this information, we already know the angle of our vector <xo, yo> is the theta. And, the new position is the new angle (alpha) + theta.

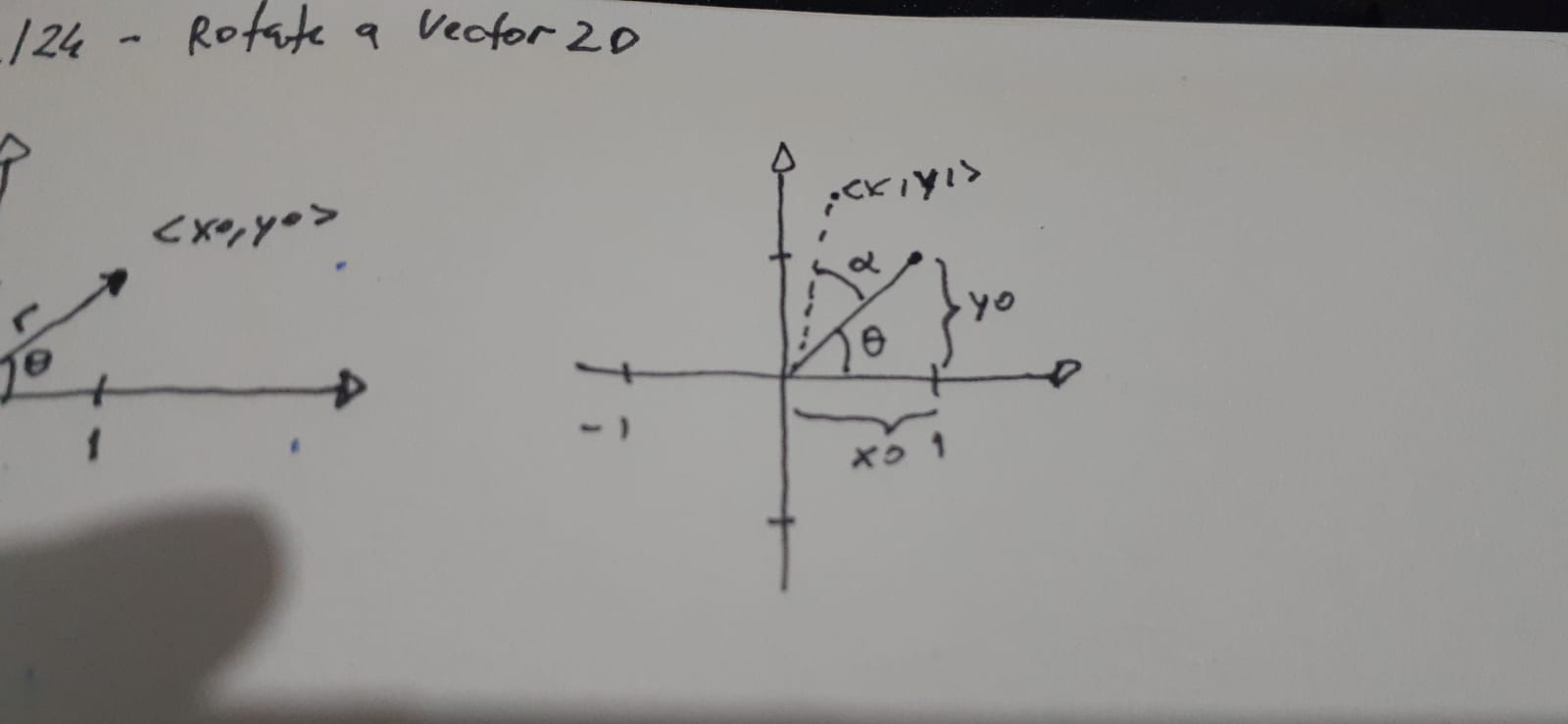
To figure out the xo value and yo value, we can use the cossine and sine by the formula:

cos(theta) = xo / r

xo = cos(theta) * r

sin(theta) = yo / r

yo = sin(theta) * r

So, xo = cos(theta) * r and yo = sin(theta) * r.

Now, we know that new angle can use the same approach. Let's see:

x1 = cos(theta+alpha) * r and y1 = sin(theta+alpha) * r.

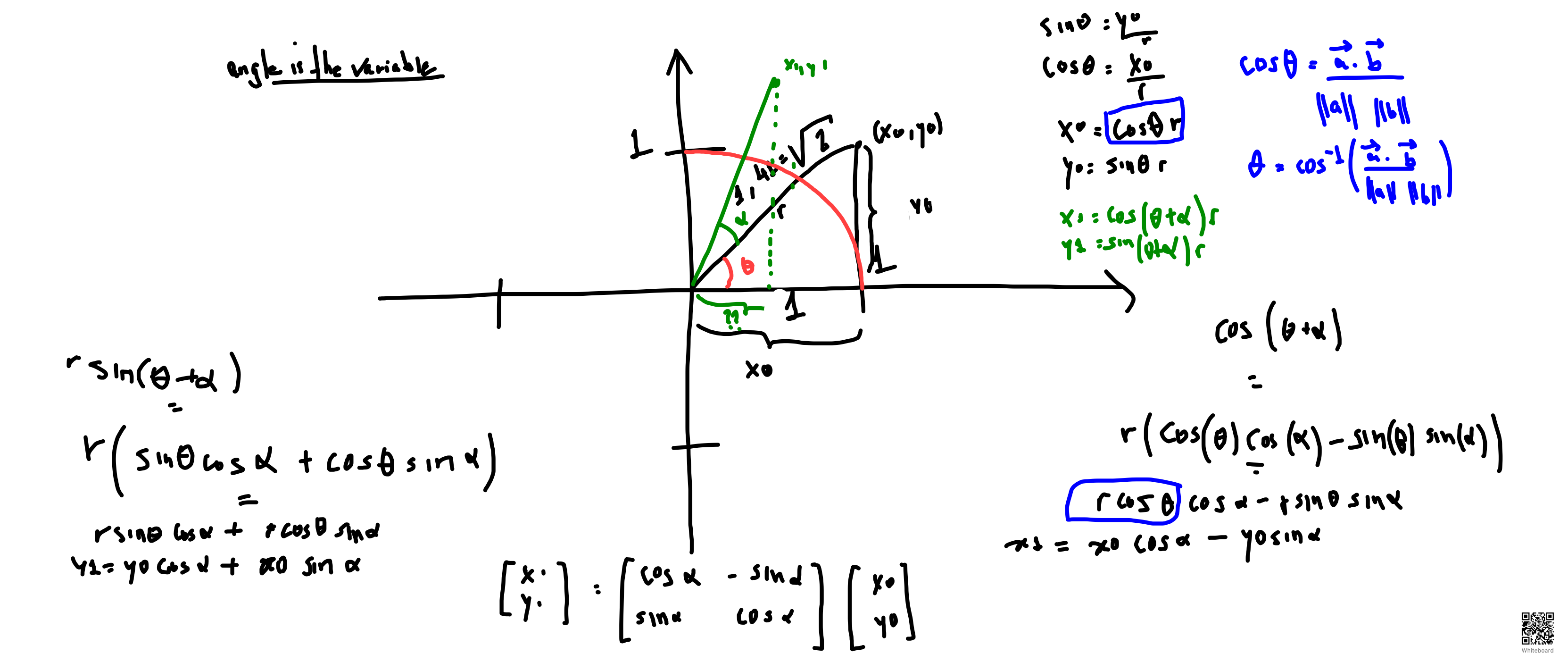
The secret here is the cos(theta+alpha) because we can use the trigonometric identities to derivate and see the raw formula.

The r * cos(theta+alpha)

= r * cos(theta) * cos(alpha) - r * *sin(theta) * sin(alpha).

If you notice, the r * cos(theta) is the same as xo. At same time, the r * sin(theta) = yo. So, the formula can be:

x1 = xo * cos(alpha) - yo * sin(alpha)

Let's do the same for the Y value.

The sin(theta+alpha) * r

= r * sin(theta) * cos(alpha) + r * cos(theta) * sin(alpha).

So, y1 = yo * cos(alpha) + xo * sin(alpha).

The final matrix results will be:

[x] = [cos(alpha) - sin(alpha)] = [xo]

[y] = [sin(alpha) cos(alpha)] = [yo]

Examples

Vector = (2, 1) Rotate = 90 degrees = PI / 2

xo = 2
yo = 1
x1 = xo * math.cos(math.pi / 2) - yo * math.sin(math.pi / 2)
x1 = -1.0
y1 = xo * math.sin(math.pi / 2) + yo * math.cos(math.pi / 2)
y1 = 2.0

How to Rotate a Vector2d

Table of Contents

Examples